limit fungsi di suatu titik

Limit Fungsi di Satu Titik

Dalam menentukan nilai limit suatu fungsi dapat dilakukan dengan beberapa cara :
a. Substitusi 

Dengan mengganti nilai x pada fungsi sesuai dengan nilai x pendekatan limit.

Contoh :

1. 1. lim_x→3 2x - 8 = 2 . 3 - 8 = -2
   2. lim_x→3 (x² + 2x + 1) = 3² + 2 . 3 + 1 = 16

b. Faktorisasi 

Digunakan apabila menggunakan cara substitusi saja menghasilkan bilangan pecahan  , yang berarti bilangan tersebut tak terdefenisi.

Contoh :

Tentukan nilai limit berikut :

• • lim_x→4  = lim_x→4 

=  (x + 4) = 4 + 4 = 8

c. Mengalikan Faktor Sekawan / Merasionalkan Penyebut

Digunakan saat bentuk fungsi berupa akar, yang bertujuan untuk menghilangkan bentuk akar sehingga menjadi lebih sederhana.

* Beberapa bentuk faktor sekawan :

• • (x - a) bentuk sekawan dari (x + a)
  • (√x - a) bentuk sekawan dari (√x + a)
  • (√x - √y) bentuk sekawan dari (√x + √y)

Mengalikan dengan faktor sekawan juga digunakan untuk merasionalkan pecahan dengan penyebut yang berbentuk akar. Kemudian agar nilai pecahannya tidak berubah pecahan semula harus dikalikan dengan pecahan yang bernilai satu.

* Beberapa bentuk merasionalkan penyebut :

• • •   =    x  
    •   =    x  
    •  =    x  

Contoh : 

lim_x→1  = lim_x→1 () x ()

=  

=  

=  

=  

=  = 

Read More

sudut

Sudut (geometri)

Lompat ke: navigasi, cari

Ruang dan besaran rotasi.

 

Untuk kegunaan lain dari sudut, lihat sudut (disambiguasi).

Sudut dalam geometri adalah besaran rotasi suatu ruas garis dari satu titik pangkalnya ke posisi yang lain. Selain itu, dalam bangun dua dimensi yang beraturan, sudut dapat pula diartikan sebagai ruang antara dua buah ruas garis lurus yang saling berpotongan. Besar sudut pada lingkaran 360°. Besar sudut pada segitiga siku-siku 180°. Besar sudut pada persegi/segi empat 360°. Untuk mengukur sudut dapat digunakan busur derajat. Tiap sudut segitiga sama sisi masing masing 60°, karena semua sudutnya sama besar maka 180° :3 = 60°. Sedangkan tiap sudut persegi 90° karena semua sudutnya juga sama besar maka 360° : 4 = 90°
NAMA-NAMA SUDUT
Sudut adalah istilah yang sangat penting dan memiliki beberapa definisi:

1. Bentuknya terbuat dari 2 garis lurus yang bertemu disebuah titik
2. Membuat jarak di antara 2 garis tersebut
3. Jumlah ukuran 2 jarak pada busur
4. Titik sudut adalah ujung kedua garis itu akan membentuk sebuah sudut

Nama sudut

Memberi nama untuk sudut dengan berbagai karakteristik:

1. Sudut 0 tidak memiliki jarak antara kedua garis
2. Sudut lancip adalah sudut antara 0 dan 89 derajat
3. Sudut siku-siku adalah sudut 90 derajat .Dua garis yang membentuk sudut 90 derajat jika tegak lurus dengan yang lain.Pembentukan simbol sudut adalah potongan kotak.Simbol itu menunjukkan jika kamu bekerja dengan sudut siku-siku.
4. Sudut tumpul adalah sudut antara 91 dan 179 derajat
5. Sudut lurus adalah sudut yang besarnya 180 derajat
6. Sudut pusat adalah sudut yang memiliki titik sudut yang terletak ditengah lingkaran
7. Sudut bersebelahan adalah sudut yang memiliki titik sudut yang sama dan satu bagian sisi yang sama(bersebelahan berarti dekat)
8. Sudut yang berseberangan dibentuk oleh 2 garis lurus menyilang dan selalu sama

Sudut 90

Sudut yang sering digunakan dalam perdagangan adalah sudut 90. Itu dapat membantu dalam pemahaman mengapa demikian. Jika 2 garis disilangkan, maka membentuk 4 sudut. Jumlah dari keempat sudut itu adalah 360. Garis utama dari jangka adalah 2 garis lurus yang mana jika 2 garis tersebut disilangkan masing-masing besar sudutnya adalah 90. Sebagian besar dan perusahaan-perusahaan mengatakan untuk membuat garis sepanjang garis utama dari jangka. Jika 2 garis disilangkan, dari keempat sudut yang terbentuk masing-masing besarnya sama jika pada setiap sudutnya besarnya 90. Sudut 90 biasa disebut sudut siku-siku. Sudut siku-siku biasanya terdapat pada bangun datar seperti segitiga siku-siku, persegi panjang dan persegi.

Read More

Garis

Garis (geometri)

Lompat ke: navigasi, cari

Contoh satu ruas garis

Tiga garis — garis merah dan biru memiliki kemiringan yang sama, sementara garis merah dan hijau memiliki persilangan y yang sama.

Garis (bahasa Inggris: line), dalam geometri Euklides, adalah sebuah lengkungan lurus. Ketika geometri digunakan untuk memodel dunia nyata, garis digunakan untuk menggambarkan objek lurus dengan lebar dan tinggi yang berbeda. Garis adalah idealisasi dari objek semacam itu dan tidak punya lebar atau tinggi dan panjangnya dianggap tak hingga
Dalam geometri, sebuah garis biasanya merupakan satu anggapan primitif dari sistem aksioma. Garis terdiri dari himpunan titik dan merupakan subhimpunan dari bidang. Dalam geometri diferensial, konsep garis digeneralisasikan menjadi geodesi. Dalam geometri sintetis, sebuah garis adalah satu anggapan lama dalam sistem Euklides, Karl von Staudt, dan David Hilbert. Sebuah garis adalah sebutan terdefinisikan dalam sistem Giuseppe Peano, Mario Pieri dan Alessandro Padoa.
Sebuah ruas garis adalah bagian dari garis yang dikelilingi oleh dua ujung berbeda dan terdiri dari setiap titik di garis antara kedua ujungnya. Tergantung cara ruas garis ini dideginisikan, satu dari dua ujung tersebut bisa jadi atau bukan bagian dari ruas garis. Dua ruas garis atau lebih bisa memiliki hubungan yang sama seperti garis, seperti paralel, perpotongan, atau kemiringan.

Read More

Titik

Titik (geometri)

Titik di dalam geometri Euclidean

Sehimpunan berhingga titik-titk (biru) di dalam ruang euclid dua dimensi.

Titik sering dipandang di dalam kerangka kerja geometri Euklides, di mana ia adalah salah satu objek yang mendasar. Euclid mulanya mendefinisikan titik secara kabur, sebagai "yang tak memiliki bagian". Di dalam ruang Euclidean dua dimensi, titik dinyatakan oleh pasangan terurut, ${\displaystyle \,(x,y)}$, bilangan, di mana bilangan pertama yang menurut konvensi menyatakan horizontal dan sering dituliskan sebagai ${\displaystyle \,x}$, dan bilangan kedua secara konvensi menyatakan vertikal dan sering dituliskan sebagai ${\displaystyle \,y}$. Gagasan ini mudah diperumum ke dalam ruang Euclid tiga dimensi, di mana titik dinyatakan oleh pasangan terurut ganda-tiga, ${\displaystyle \,(x,y,z)}$, dengan bilangan tambahan ketiga menyatakan kedalaman dan diwakili oleh z. Perumumuman lebih lanjut dinyatakan oleh pasangan terurut ganda-n,${\displaystyle \,(a_{1},a_{2},...,a_{n})}$ di mana n adalah dimensi ruang tempat titik berada.
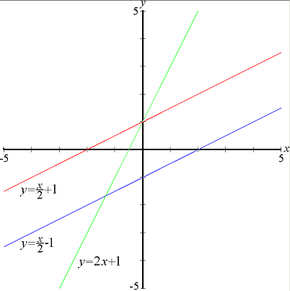
Banyak objek yang dibangun di dalam geometri Euclid terdiri dari tak hingga banyaknya kumpulan titik-titik yang sesuai dengan aksioma-aksioma tertentu. Hal ini biasanya dinyatakan oleh himpunan titik-titik; misalnya, garis adalah himpunan tak hingga banyaknya titik-titik yang berbentuk ${\displaystyle \,L=\lbrace (a_{1},a_{2},...a_{n})|a_{1}c_{1}+a_{2}c_{2}+...a_{n}c_{n}=d\rbrace }$, di mana ${\displaystyle \,c_{1}}$ melalui ${\displaystyle \,c_{n}}$ dan ${\displaystyle \,d}$ adalah konstanta dan n adalah dimensi ruang. Juga terdapat konstruksi-konstruksi serupa yang mendefinisikan bidang, ruas garis, dan konsep-konsep lainnya yang saling berkaitan.
Selain mendefinisikan titik dan konstruksi yang berkaitan dengan titik, Euclid juga mempostulatkan gagasan kunci tentang titik; dia mengaku bahwa dua titik sembarang dapat dihubungkan oleh sebuah garis lurus. Ini dapat dengan mudah diperiksa di bawah perluasan modern geometri Euklides, dan menyisakan dampak-dampak pada introduksinya, mengizinkan konstruksi hampir semua konsep geometri tentang waktu. Tetapi, postulat Euclid tentang titik tidak pernah lengkap, tidak pula definitif, karena dia kadang-kadang mengasumsikan fakta tentang titik yang tidak mengikuti secara langsung aksioma-aksiomanya, misalnya pengurutan titik-titik pada garis atau keujudan titik-titik tertentu. Meskipun demikian, perluasan modern sistem ini berhasil menghilangkan anggapan-anggapan ini.

Read More

trigonometri

Integral Tak tentu

Rumus integral bentuk baku

 

 

Tidak afdol dong belajar matematika tanpa melihat contoh soal dan pembahasan materi integralnya, yuk perhatikan contoh soal berikut :

Rumus tambahan

dengan a = konstanta

Integral dengan cara subtitusi

yang dimaksud dengan integral cara subtitusi yaitu meng-integrasikan fungsi yang berbentuk seperti integral baku, dengan mensubtitusikannya, seperti contoh berikut :

ganti x dengan ( 3 + 6x ) agar sama, dengan cara mendeferensialkan fungsi yang terletak pada dalam kurung.

Rumus integral subtitusi

Integral Trigonometri

Berikut tabel rumus integral trigonometri yang dapat membantu kita dalam menyelesaikan persoalan-persoalan integral trigonometri.

sebenarnya masih ada sih contoh soal integral trigonometri yang sudah disertai pembahasannya tapi berhubung sudah malam dan hampir pagi maka postingan kali ini admin cukupkan, terus contohnya mana ? tenang saja ebooknya sudah admin uploadkan untuk kalian mulai dari pembahasan awal tadi.

 

Read More

Keterbagian

DEFINISI KETERBAGIAN

Pembagian bilangan bulat merupakan bahan pelajaran matematika yang sudah diberikan di sekolah dasar. Bahan pelajaran ini diperluas penggunaannya sampai pada pemfaktoran prima, faktor persekutuan terbesar (FPB), kelipatan persekutuan terkecil (KPK), dan keterbagian oleh bilangan tertentu (misalnya keterbagian oleh 2,3, atau 9). Untuk memberikan dasar atau landasan yang lebih kuat kepada guru matematika di sekolah, maka mereka perlu  belajar lebih mendalam tentang konsep-konsep dasar keterbagian.

Keterbagian (divisibility) merupakan dasar pengembangan teori bilangan, sehingga konsep-konsep keterbagian akan banyak digunakan didalam sebagian besar uraian atau penjelasan matematis tentang pembuktian teorema. Keadaan inilah yang memberikan gagasan tentang perlunya definisi keterbagian. Keterbagian atau divisibility adalah sudut pandang matematika yang mempelajari suatu bilangan yang habis oleh bilangan lain.

II.        SIFAT-SIFAT KETERBAGIAN

Teorema 1                                                         

Jika a, b, dan c adalah bilangan bulat dengan a│b dan  b│c maka a│c.

Bukti

a│b dan b│c maka menurut Definisi, terdapat bilangan bulat m dan n sedemikian sehingga   c = bn = (am)n = a(mn). Jadi, c = a(mn). Untuk suatu mn = p  anggota bilangan Bulat maka c = ap Akibatnya menurut Definisi, a│c.

Teorema 2

Jika a, b, dan c adalah bilangan bulat dengan c│a dan c│b maka c│(am+bm). untuk suatu m,n anggota bilangan bulat.

Bukti

            c│a dan c│b maka terdapat bilangan bulat x dan y sedemikian sehingga a =cx dan b =cy

Sehingga, am = c(xm) dan  bn =c(yn). untuk suatu xm = p dan (yn)=q, Maka:

 am + bn = c(p+q). Akibatnya,c│(am+bn).

Teorema 3 (Buchmann, 2002: 3)

a.          Jika a│b dan b ≠ 0 maka |a| ≤ |b|.

b.         Jika a│b dan b│a maka |a| = |b|.

Bukti

a.          Jika  a│b dan b ≠ 0 maka menurut Definisi, terdapat  m ≠ 0

sedemikian sehingga b = am.

Karena b = am maka |b| = |am| ≥ |a| sehingga, |a| ≤ |b|.

b.         Andaikan  a│b dan b│a.  Jika a = 0 maka b = 0 dan jika a ≠ 0  maka b ≠ 0.

Selanjutnya,

Jika  a ≠ 0 dan  b ≠ 0 maka sesuai dengan Teorema

Read More